在使用sklearn时如何选择合适的分类器

发表于 | 分类于 ，

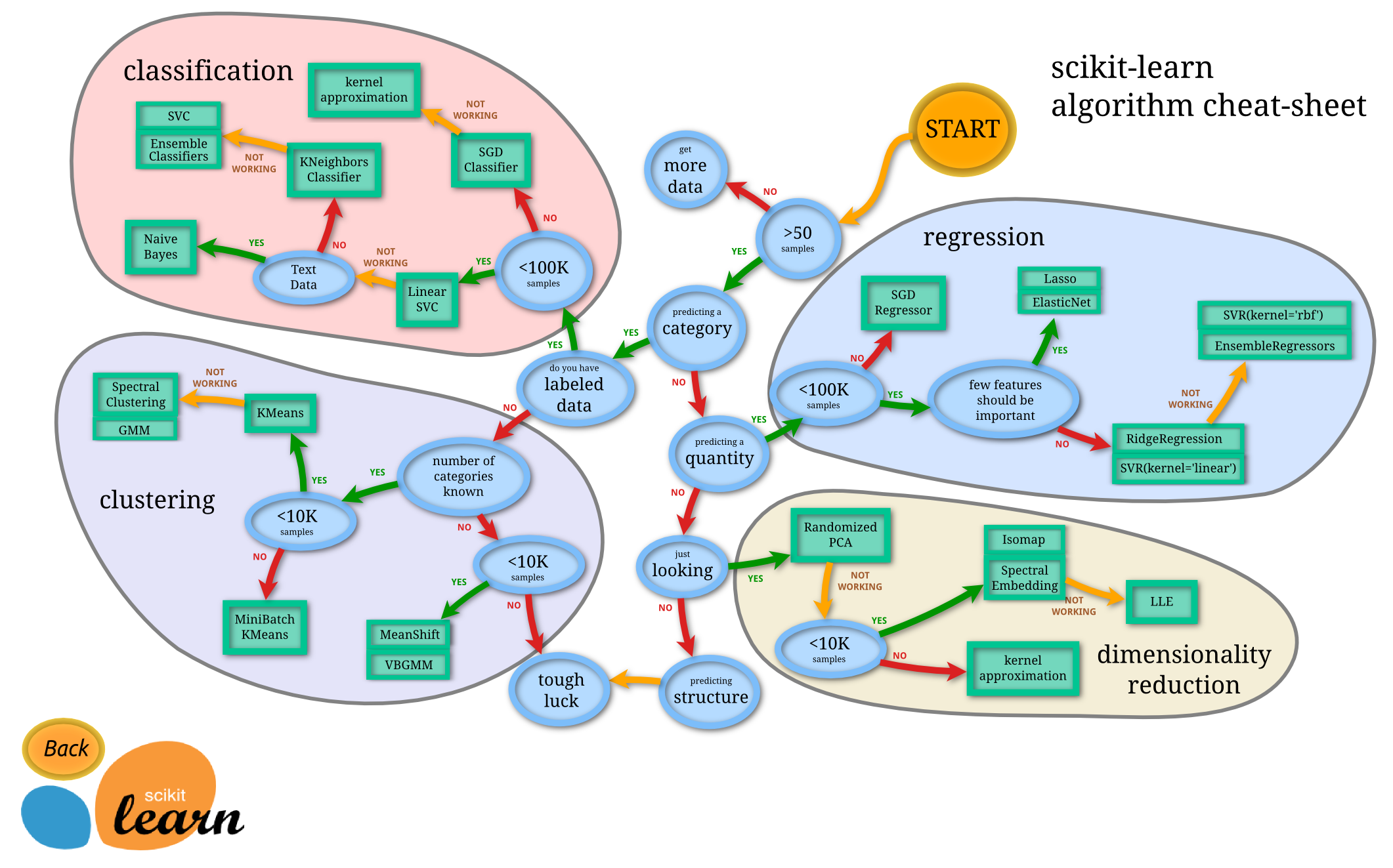
选择合适的机器学习算法

All models are wrong, but some models are useful. — George Box (Box and Draper 1987)

根据No free lunch theorem，在机器学习中，不存在一个在各方面都最好的模型/算法，因为每一个模型都或多或少地对数据分布有先验的统计假设。取所有可能的数据分布的平均，每个模型的表现都一样好（或者一样糟糕）。因此，我们需要针对具体的问题，找到最好的机器学习算法。

下面是可能的效果图：

数据分析（Exploratory Data Analysis）

在选择具体的算法之前，最好对数据中每一个特征的模式和产生原理有一定的了解：

  • 特征是连续的（real-valued）还是离散的（discrete）？
  • 如果特征是连续的，它的直方图（histogram）长什么样？它的mean和variance是如何分布的？
  • 如果特征是离散的，不同的特征值之间是否存在某种顺序关系？例如，豆瓣上从1星到5星的打分，虽然是离散数据，但有一个从低到高的顺序。如果某个特征是“地址”，则不太可能存在一个明确的顺序。
  • 特征数据是如何被采集的？

特征工程（Feature Engineering）

特征工程（根据现有的特征，制造出新的、有价值的特征）决定了机器学习能力的上限，各种算法不过是在逼近这个上限而已。不同的机器学习算法一般会有其对应的不同的特征工程。在实践中，特征工程、调整算法参数这两个步骤常常往复进行。

由简至繁：具体算法的选择

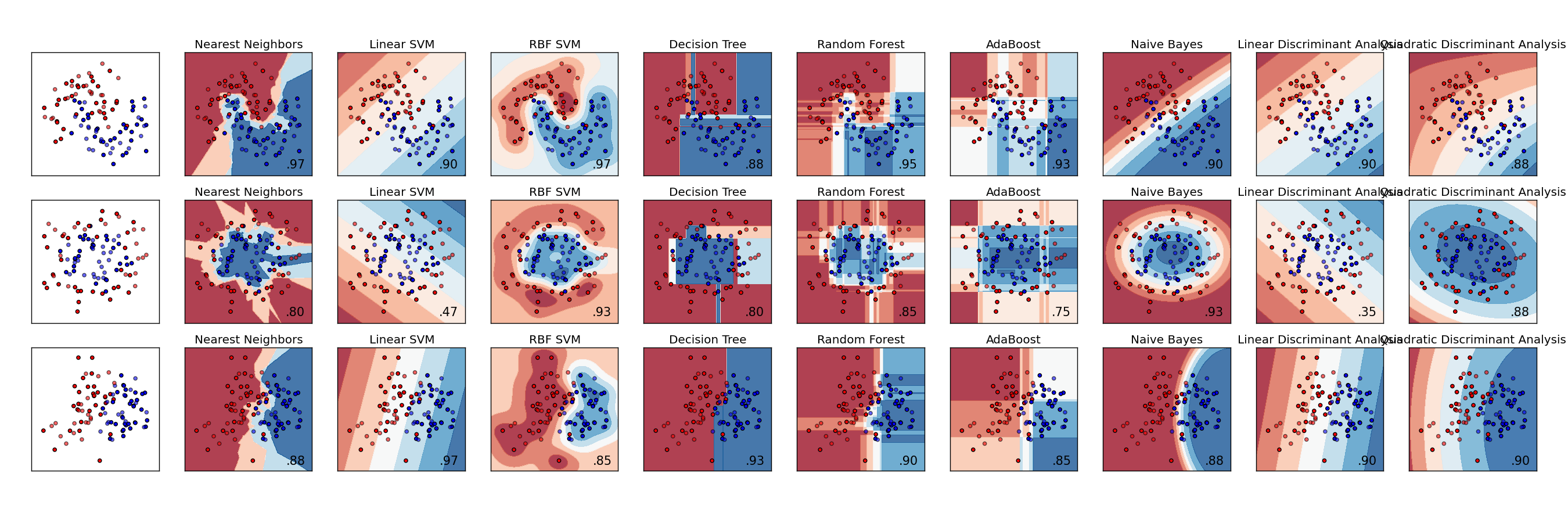
sklearn包括了众多机器学习算法。为了简化问题，在此只讨论几大类常见的分类器、回归器。至于算法的原理，sklearn的文档中往往有每个算法的参考文献，机器学习的课本也都有所涉及。

General Linear Models

最开始建立模型时，我个人一般会选择high bias, low variance的线性模型。线性模型的优点包括计算量小、速度快、不太占内存、不容易过拟合。

常用线性回归器的有Ridge（含有L2正则化的线性回归）和Lasso（含有L1正则化的线性回归，自带特征选择，可以获得sparse coefficients）。同时，如果对于超参数没有什么特别细致的要求，那么可以使用sklearn提供的RidgeCV和LassoCV，自动通过高效的交叉验证来确定超参数的值。

假如针对同一个数据集X（m samples n features），需要预测的y值不止一个（m samples n targets），则可以使用multitask的模型。

线性分类器中，最好用的是LogisticRegression和相应的LogisticRegressionCV。

SGDClassifier和SGDRegressor可以用于极大的数据集。然而，如果数据集过大的话，最好从数据中取样，然后和小数据一样分析建模，未必一开始就要在整个数据集上跑算法。

Ensemble Methods

ensemble能够极大提升各种算法，尤其是决策树的表现。在实际应用中，单独决策树几乎不会被使用。Bagging（如RandomForest）通过在数据的不同部分训练一群high variance算法来降低算法们整体的variance；boosting通过依次建立high bias算法来提升整体的variance。

最常用的ensemble算法是RandomForest和GradientBoosting。不过，在sklearn之外还有更优秀的gradient boosting算法库：XGBoost和LightGBM。

BaggingClassifier和VotingClassifier可以作为第二层的meta classifier/regressor，将第一层的算法（如xgboost）作为base estimator，进一步做成bagging或者stacking。

支持向量机（SVM）

SVM相关的知识可以参考Andrew Ng教授在Coursera上的CS229（有能力的可以去看youtube或者网易公开课上的原版CS229）。svm的API文档很完善，当一个调包侠也没有太大困难。不过在大多数的数据挖掘竞赛（如kaggle）中，SVM的表现往往不如xgboost。

神经网络（Neural Network）

相比业内顶尖的神经网络库（如TensorFlow和Theano），sklearn的神经网络显得比较简单。个人而言，如果要使用神经网络进行分类/回归，我一般会使用keras或者pytorch。

附上sklearn库之各分类算法简单应用

KNN

1
2
3
4
5
6
7
8
9
10
from sklearn.neighbors import KNeighborsClassifier
import numpy as np
def KNN(X,y,XX)：#X,y 分别为训练数据集的数据和标签，XX为测试数据
    model = KNeighborsClassifier(n_neighbors=10)#默认为5
    model.fit(X,y)
    predicted = model.predict(XX)
    return predicted

SVM

1
2
3
4
5
6
7
8
9
from sklearn.svm import SVC
def SVM(X,y,XX):
    model = SVC(c=5.0)
    model.fit(X,y)
    predicted = model.predict(XX)
    return predicted

SVM Classifier using cross validation

1
2
3
4
5
6
7
8
9
10
11
12
13
def svm_cross_validation(train_x, train_y):    
    from sklearn.grid_search import GridSearchCV    
    from sklearn.svm import SVC    
    model = SVC(kernel='rbf', probability=True)    
    param_grid = {'C': [1e-3, 1e-2, 1e-1, 1, 10, 100, 1000], 'gamma': [0.001, 0.0001]}    
    grid_search = GridSearchCV(model, param_grid, n_jobs = 1, verbose=1)    
    grid_search.fit(train_x, train_y)    
    best_parameters = grid_search.best_estimator_.get_params()    
    for para, val in list(best_parameters.items()):    
        print(para, val)    
    model = SVC(kernel='rbf', C=best_parameters['C'], gamma=best_parameters['gamma'], probability=True)    
    model.fit(train_x, train_y)    
    return model

LR

1
2
3
4
5
6
7
8
9
from sklearn.linear_model import LogisticRegression
def LR(X,y，XX):
    model = LogisticRegression()
    model.fit(X,y)
    predicted = model.predict(XX)
    return predicted

决策树（CART）

1
2
3
4
5
6
7
8
from sklearn.tree import DecisionTreeClassifier
def CTRA(X,y,XX):
    model = DecisionTreeClassifier()
    model.fit(X,y)
    predicted = model.predict(XX)
    return predicted

随机森林

1
2
3
4
5
6
7
8
from sklearn.ensemble import RandomForestClassifier
def CTRA(X,y,XX):
    model = RandomForestClassifier()
    model.fit(X,y)
    predicted = model.predict(XX)
    return predicted

GBDT

(Gradient Boosting Decision Tree)

1
2
3
4
5
6
7
8
from sklearn.ensemble import GradientBoostingClassifier   
def CTRA(X,y,XX):
    model = GradientBoostingClassifier()
    model.fit(X,y)
    predicted = model.predict(XX)
    return predicted

朴素贝叶斯

一个是基于高斯分布求概率，一个是基于多项式分布求概率，一个是基于伯努利分布求概率。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
from sklearn.naive_bayes import GaussianNB
from sklearn.naive_bayes import MultinomialNB
from sklearn.naive_bayes import BernoulliNB
def GNB(X,y,XX):
    model =GaussianNB()
    model.fit(X,y)
    predicted = model.predict(XX)
    return predicted
def MNB(X,y,XX):
    model = MultinomialNB()
    model.fit(X,y)
    predicted = model.predict(XX
    return predicted
def BNB(X,y,XX):
    model = BernoulliNB()
    model.fit(X,y)
    predicted = model.predict(XX
    return predicted